Matlab Object-Oriented Programming and Classes
Matlab object-oriented programming is a bit awkward and unlike most other
OO languages, but still has some of the elements that make OO programming
useful. Here I will describe some aspects of Matlab objects, using a class
to construct a k-nearest neighbor classifier as a working example.
Getting started
First, download the course code into a directory, say,
~ihler/Code/cs178/.
You should see a number of files and directories created there;
for the purposes of this handout, the relevant directory to have is the
@knnClassify directory, which contains the files for the
classifier.
You should make sure you are either in the directory you downloaded the
files to, or add it to your Matlab path. For example, use
>> addpath ~ihler/Code/cs178
to add that directory to Matlab's path. Note that you should not
be in the @knnClassify directory, nor should you add
it to the path -- only its parent directory.
We will use "old style" Matlab objects, which consist of a directory
(@-something), which uses one file per member function (private functions
go in a further subdirectory called private). While there are
some drawbacks to this type of object (and Matlab has since updated
their object representations to be more flexible and give them
more capabilities), this is the type
that is also compatible with Octave, which is useful also.
Using the class
To create an object of the class type, you can simply call the constructor.
To find out its usage, use help:
>> help knnClassify
knnClassify(X,Y,...) : create k-nearest-neighbors classifier
takes no arguments, or training data to be used in constructing the classifier
alpha: weighted average coefficient (Gaussian weighting); alpha=0 => simple average
and we can then use it:
>> Xtr = rand(5,3), % Create feature matrix of 5 data points with 3 features each
Xtr = % (just in case you want to use the same numbers I do...)
0.4898 0.2760 0.4984
0.4456 0.6797 0.9597
0.6463 0.6551 0.3404
0.7094 0.1626 0.5853
0.7547 0.1190 0.2238
>> Ytr = [0 0 0 1 1]'; % and a corresponding Ytrain of target classes
>> knn = knnClassify(Xtr,Ytr,3), % Create 3-nearest-nbr classifier with those data
KNN Classifier, 2 classes, K=3
Now, to find out what methods are available for a given class,
we can use the methods command to list them:
>> methods knnClassify
Methods for class knnClassify:
auc err predict setClasses
confusion getClasses predictSoft setK
display knnClassify roc train
Our most typical operations will be train and predict, which
train a model on training data, and predict the current model on new data, respectively.
Typically, when constructor functions accept training data, they simply call the
train function.
To see what parameters train takes, we need to differentiate which
train we mean:
>> help knnClassify/train
knn=train(knn,Xtrain,Ytrain) : Batch training for knn; just memorize data
Using this calling pattern, we can re-train the model with e.g.,
>> knn = train(knn, Xtr,Ytr);
and predict with
>> Xte = rand(2,3), % Make two test data points (same # of features!)
Xte =
0.7513 0.5060 0.8909
0.2551 0.6991 0.9593
>> Yte = [0 1]'; % and some test target values for goot measure
>> Yhat= predict(knn,Xte), % Make prediction for those points:
Yhat =
0
0
Two points are worth noting: First, member functions are typically called by
passing the object as the first argument of the function. They can also be
called in a more typical format, knn.train(Xtr,Ytr), but both are
implemented in exactly the same way.
Second, functions that modify the class in some way (such as train)
should actually return (and set) the object variable. Matlab cannot generally
update variables by reference (recent object changes relax this point), and
so the object must be returned in order to modify it.
We can also use accessor functions to get or set object properties, such as:
>> knn = setK(knn, 1), % Change to a 1-nearest nbr classifier
KNN Classifier, 2 classes, K=1
Again, we actually return the modified object variable, and set kdd
to be equal to the returned value.
The object constructor
Let's take a closer look at how the constructor function
knnClassify.m works. First, here is the file header:
function obj = knnClassify(Xtr,Ytr,K)
% knnClassify([X,Y,K]) : create k-nearest-neighbors classifier
% takes no arguments, or training data to be used in constructing the classifier
The first line declares the function itself, and any returned variables.
The first set of comments in the file are output for the help
command (help knnClassify), and should contain basic usage information.
Default values are a bit awkward; typically, you can check how many variables
were passed in and fill in any missing ones (positional defaults):
if (nargin < 3) K = 1; end;
Another typical approach is to require that the caller pass an empty matrix,
which can be tested for and filled in with a default value.
The basic form of an object is simply a Matlab structure with a bit of extra
gloss on top; we declare the member variables as if it were a structure, and
then call a function to define it as a class:
obj.K=K; obj.Xtrain=[]; obj.Ytrain=[]; obj.classes=[];
obj=class(obj,'knnClassify');
I usually do this immediately with empty values, since the variable fields
must always be declared in the same order. Note also that return values are
specified by name, so if obj is listed as the return variable, whatever
variable is called obj when the function ends is returned.
I typically also allow train to be called automatically by just passing
the data into the constructor:
if (nargin > 0)
obj = train(obj,Xtr,Ytr);
obj = setK(obj,K);
end;
Or, these can be called manually after.
As an aside, Matlab objects can be converted into structures, allowing their
internal data to be accessed by anyone:
>> s = struct(knn),
s =
K: 1
Xtrain: [5x3 double]
Ytrain: [5x1 double]
classes: [2x1 double]
This can be useful if you're trying to access something in an object while debugging,
but is usually non-reversible, i.e., it is difficult to modify s and transform it
back to an object afterwards.
The train function
Training for a k-nearest neighbor classifier is trivial; we simply memorize the data:
function obj=train(obj, Xtr,Ytr)
% knn=train(knn,Xtrain,Ytrain) : Batch training for knn; just memorize data
obj.Xtrain = Xtr;
obj.Ytrain = Ytr;
obj.classes= unique(Ytr);
One minor point -- I always keep a column vector obj.classes in each classifier.
The internal implementation of the classifier predicts a positive integer 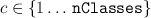 ,
and then returns
,
and then returns obj.classes(c). This way, the class values can be
non-consecutive, non-standard, and even of different Matlab types (characters or whatever)
without any difficulty. Some classifiers are implemented specifically for binary
classification problems, in which case we can simply check that the number of classes is only
two.
The predict function
In order to predict with a k-nearest neighbor classifier, we simply search the stored
training data for the nearest points, in terms of their sum of squared differences.
The file header,
function Yte = predict(obj,Xte)
% Yhat = predict(knn, Xtest) : make a nearest-neighbor prediction on test data
[Ntr,Mtr] = size(obj.Xtrain); % get size of training, test data
[Nte,Mte] = size(Xte);
K = min(obj.K, Ntr); % can't have more than Ntrain neighbors
Yte = repmat(obj.Ytrain(1), [Nte,1]); % make Ytest the same data type as Ytrain
gets the number of training and test data, and their dimensions ($M$, which should be the
same for both), and makes sure $K$ is valid. We pre-initialize Yte by
copying (repmat = repeat matrix) one of the training data to the correct size;
pre-allocating the correct vector size helps Matlab avoid constantly re-allocating
memory for Yte,
and using repmat ensures it has the right variable type.
Next, for each test data point, we compute the distance from all training data,
for example:
for i=1:Nte, % For each test example:
dist=zeros(Ntr,1); % pre-allocate a distance vector
for j=1:Ntr, % and compute distance from all Ntr training data
dist(j)=sum( (obj.Xtrain(j,:)-Xte(i,:)).^2 );
end;
end;
However, this turns out to be awfully slow; Matlab is interpreted, and often has
trouble performing for-loops quickly. For better performance, you may
learn to ``vectorize'' your calculations, performing them all in one step:
dist = sum( (obj.Xtrain - repmat(Xte(i,:),[Ntr,1]) ).^2 , 2);
This copies the Xte data point to be the same size as Xtrain,
then subtracts the two matrices, squares the entries (element-wise), and sums
them over their 2nd dimension (the features), leaving a column-vector of distances
exactly like the for-loop above. Even harder to read but slightly faster still
is to use the bsxfun function, which performs operators on differently-sized
matrices (so that you don't need to use repmat to copy the data point):
dist = sum( bsxfun( @minus, obj.Xtrain, Xte(i,:) ).^2 , 2);
All this is useful if you are finding Matlab very slow, but takes a while to get used to.
Finally, we find the $K$ nearest data examples, and find the majority vote among them:
[dst,idx] = sort(dist); % find nearest neighbors over Xtrain
idx=idx(1:K); % keep nearest K data points
nClasses=length(obj.classes);
count = zeros(1,nClasses); % count up how many in each class
for c=1:nClasses, count(c)=sum( obj.Ytrain(idx)==obj.classes(c) ); end;
[nil cMax] = max(count); % find the (position of the) largest #
Yte(i) = obj.classes(cMax); % and save the prediction
A useful trick here -- both sort and max can return both the
sorted / maximum value (first return value) and the position of those values
(as the second return value). So idx is a list of the training data points
in order from nearest to farthest, and cMax is the index of the class with
the largest count value.
Also, obj.Ytrain(idx)==obj.classes(c) is a binary vector, with "1"
when the equality condition is satisified and "0" if not. Then, sum
counts up the number of "1" entries.
Measuring errors
A few functions are common to almost all predictors; for example,
frequently, we want to evalute the error rate, measuring how often our model makes
incorrect predictions on a data set (e.g., the training or validation error).
Functions like err do this easily:
>> J = err(knn, Xte, Yte), % evalute the empirical error rate on these data
J =
0.5000
To get more information, we may want to look at the confusion matrix:
>> C = confusion(knn, Xte, Yte), % evalute the confusion matrix:
C =
1 0 % one true class zero (column), predicted 0 (row)
1 0 % one true class zero (column), predicted 1 (row)
Similar functions (mse, etc.) are found in regression classes.
Many classifiers also support soft predictions, which express some level
of confidence in the possible outcomes. For example, in kNN, we might return
the fraction of the $K$ neighbors in each class (rather than just the decision);
predictSoft returns a length-nClasses vector of such confidences
for each data point:
>> knn = setK(knn, 3); % poinless for k=1...
>> ySoft = predictSoft(knn,Xte), % make soft predictions:
ySoft =
0.6667 0.3333 % test point 1 has 66% confidence in class 0
1.0000 0 % test point 2 has 100% confidence in class 0
These soft scores are useful in computing, for example, ROC curves
(note that this only works for binary classifications):
[fpr,tpr,tnr] = roc(knn,Xte,Yte); % find info for ROC curve:
plot(fpr,tpr,'-'); % (not very interesting for these data, though...)
and the area under the curve can be computed with auc.m.
