
|
|
Projects /
Event detection and modeling of count-based data This page contains links to code from several papers on automatic event detection in data consisting of discrete counts, using variants of Poisson processes to model the underlying phenomena. Data examined include (a) counts of entries and exits through one or more doors of a UCI campus building, captured via a wireless optical sensor (image, right; data available from the UCI ML repository); (b) vehicle counts collected via loop sensor data on the I-405 freeway, collected by CalTrans (data available from CalTrans' website); (c) traffic accident data (date and time of accident report) from North Carolina. Markov-Modulated Poisson ProcessWork with Padhraic Smyth and Jon Hutchins at UCI; published in SIGKDD 2006. Matlab code available here. 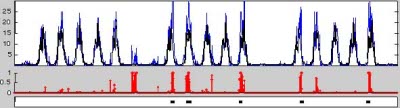 This work describes a discrete-time model, in which the data are modelled as consisting of the superposition of "normal" behavior, represented using a Poisson process, and "event" behavior consisting of increases (or more rarely, decreases) in the number of counts observed. The event behavior is captured using a Markov chain model to capture the idea of event persistence, allowing the model to find slight but sustained changes in activity and more accurately estimate the duration of a detected event. An example is shown at right, where the blue curve shows the observed counts, black the estimated normal profile; red bars show the estimated probability of an event at each time, and the bottom-most panel shows a partial ground truth of known events, held out from the model for validation purposes. Dirichlet Process Mixture ModelSorry; code is not yet available. |