• login

Current research projects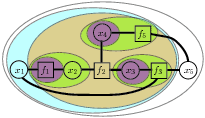

Cluster Trees for Adaptive Inference -- We use a cluster tree formalism (specifically an RC-Tree data structure) to organize the process of inference in factor graphs. This enables us to rapidly find changes and update results when small changes are made to the model.

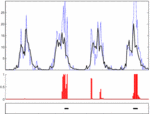Statistical models for event detection in count data -- Automatic event detection in data consisting of discrete counts, using variants of Poisson processes to model the underlying (non-event) phenomena. The methods produce a probabilistic model of "normal" behavior (useful for compression, visualization, and planning), and identify periods of anomalous measurement periods. These events can be flagged for further scrutiny, or for "known events" can provide estimates of the total associated counts as (for example) an indicator of popularity. Multiple data sources can be combined to estimate indirectly observed variables, such as total building occupancy.

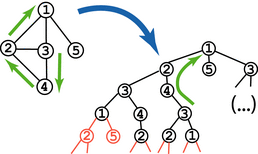Belief propagation -- Understanding the behavior of belief propagation, one of the most popular methods of approximate, variational inference in graphical models. Our research has developed convergence conditions for the algorithm, bounds on the approximation error in the estimated marginal distributions, and theoretical analysis of message errors due to quantization, message censoring, or other sources.

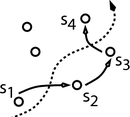Sensor networks and distributed inference -- As technology improves, we are increasingly able to monitor our environment with "smart" sensors which observe their surroundings, process information locally, and pass that information on via wireless communications. Such sensors form the basis of many types of environmental awareness, from understanding patterns of aggregate behavior such as traffic to real-time monitoring and tracking.

Nonparametric representations for probabilistic inference -- Sample based representations for probabilistic uncertainty are popular in both static and dynamic models. Kernel density estimation techniques, for example, can be applied to estimate information content, learn predictors, and represent multi-modal uncertainty without strong modeling assumptions. In dynamic problems, such as nonlinear state space tracking, particle filtering provides similarly flexible representations of uncertainty. Nonparametric belief propagation combines both techniques to provide an extension of particle filtering to more general graphs.